Se basa en un fenómeno físico resonante. La frecuencia de salida generalmente depende de la magnitud de interés que afecta a la frecuencia de oscilación.
Cualquiera de estos sensores auto resonantes requieren de un frecuencímetro, se puede crear con osciladores armónicos o de relajación, en los armónicos hay una energía almacenada por ejemplo energía cinética pasa a energía potencial, en los de relajación hay una única forma de almacenamiento y esta energía se disipa periódicamente.
El sensor autorresonante es utilizado como componente de control de la frecuencia de circuitos osciladores, convirtiendo las vibraciones mecánicas en voltajes eléctricos a cierta frecuencia.
En estos sensores no es necesario un convertidor A/D, sin embargo si se necesita una magnitud de referencia bien conocida, en este caso el oscilador del que se obtiene la base de tiempos, generalmente estos son de cuarzo y puedes sufrir alteraciones por temperatura e imperfecciones en el material.
El sensor resuena a frecuencias de la banda audible. Funciona con un hilo de reluctancia variable y se utiliza comúnmente para medir deformaciones, por lo que mide variables como son la fuerza, masa y la longitud. Utiliza el principio del módulo de Young para hacer estas mediciones.
Fig.7: Sensor Galgas Acústicas, Medidor de Fuerza
Su funcionamiento se basa en la modificación de las propiedades acústicas del material deformado. Para calcular la deformación se compara con una muestra del material sin deformar.
La menor frecuencia de oscilación transversal de una cuerda vibrante viene dada por:
l: longitud
F: fuerza mecánica al que esta sometido
Al aplicar una fuerza en uno de los extremos, la frecuencia de oscilación resultante es directamente proporcional.
Generalmente en este tipo de sensores se mide la deformación que sufre la cuerda cuando se le es aplicada una fuerza.
Para medir deformaciones, es necesario aplicar el modulo de Young. Donde E (modulo de Young) es la tensión aplicada al material sobre la deformación que sufre a causa de esta tensión.
E: modulo de youngA: es la sección transversal del hilo
F: es la fuerza alicada
ε:es la deformacion
ε:es la deformacion
Si despejamos F de la ecuación (1) tenemos que
Reemplazando (13) en (12):
Y por lo tanto ε :


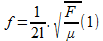
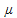
/Sensores%20digitales_html_74d01e1.gif)

































































