Demostración de la frecuencia de oscilación transversal de una cuerda vibrante, y la velocidad de propagación:
Considerando una cuerda de densidad lineal µ, si tomamos un tramo de la cuerda entonces tendremos que:
Suponiendo que los ángulos θ1 y θ2 son pequeños. Entonces podemos aproximar:
Si además suponemos que la tensión es mucho mayor que el peso de la cuerda entonces las 2 fuerzas F1 y F2 son aproximadamente iguales en módulo pero con direcciones distintas.
Además debe cumplirse la ley de Newton que dice que la sumatoria de las fuerzas debe ser igual a la masa por la aceleración.
La sumatoria de las fuerzas en y es:
Reemplazando (3) en (5)
El aumento en la fuerza vertical es en una cantidad diferencial. Por lo tanto
Si ahora unimos (4) y (6) tenemos que:Para que “y” presente movimiento ondulatorio, debía cumplir la siguiente ecuación diferencial:
Siendo "v" la velocidad de propagación de la onda.
Si observamos las ecuaciones (8) y (7) podremos ver que son muy similares.
Despejando:
Por último la velocidad de propagación de una onda está dada por:
Como es una cuerda amurada en sus dos extremos, al aplicarle una frecuencia de oscilación aparecerán nodos en la cuerda dependiendo de la longitud de onda. La longitud de onda entonces está definida por:Por lo tanto reemplazado (3) en la ecuación anterior (2) tenemos que la velocidad de propagación es:
La mínima frecuencia será cuando N=1, lo que significa que los únicos nodos son los de los extremos. Llegando entonces a la ecuación















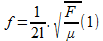
No hay comentarios:
Publicar un comentario